背景
在“ 探索计算数论(第1部分) ”我写了一篇关于黄金产生的碱基序列,称半素的二进制序列的另一种方式的非有序的方式。本文提出了一种产生并同时订购半贷二进制序列的方法。半素序列的研究是资源密集型的。下面图表1呈现用于产生在订购过程的每一个步骤,也可以作为对本文内容的表中使用的表的时间资源。笔记本式计算机上生成这些次运行的其他应用,而不是在一个实时或优化的基准系统。这只是时间的一般参考,你可以期望从这些时间很大的差异,如果你决定重新生成表。
计算
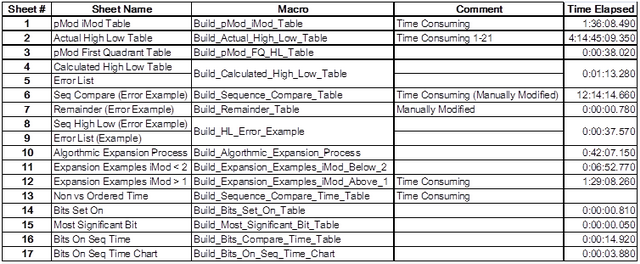
下面的数学关系将在本文中使用和下面的删节图表2说明了什么,我会期内“PMOD IMOD表”这种关系。
- pBase1 =任意素数<pBase2
- pBase2 =任何素数> pBase1
- N = pBase2国防部pBase1
- PMOD = N - 1
- IMOD =(pBase1国防部N)国防部PMOD
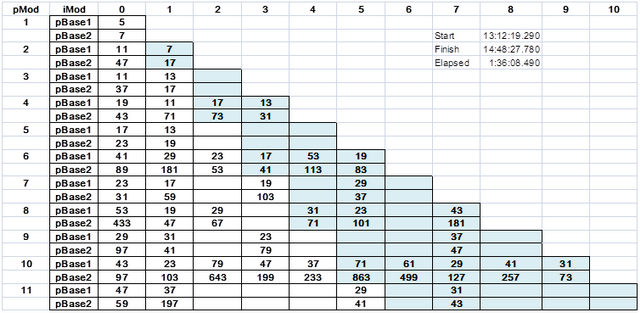
在图表2注意上面的素数2和未使用3。这些素数{2,3}和总理对,其中IMOD = 0或1产生,这将在本文后面呈现琐碎的剩余物。还要注意的最大公约数(GCD)以下关系:
-
如果GCD(N,IMOD)!= 1,则对{pBase1,pBase2}不存在。
例如:N = 10,PMOD = 9那么x =不存在对用于IMOD = {2,4,5,6,8}
表3是“实际的高低压表”,并通过检查实际的二进制序列产生的。
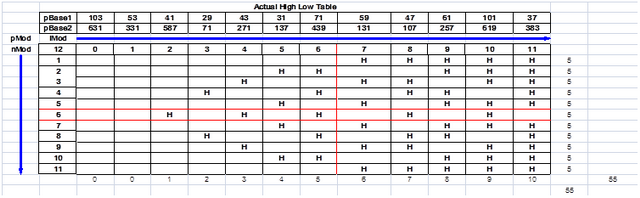
上面的图表3有以下关系:
-
NMOD =若干> 0和<PMOD代表之一的序列内的残基的增加,其中H(高)= 1和空白(低)= 0
- 如果IMOD = 0或1,则ΣnMod= 0每IMOD
- 如果IMOD> 1,则ΣnMod= IMOD - 1%的IMOD
- ΣiMod=(PMOD-2-X)/ 2%NMOD
- ΣΣiMod=ΣΣnMod=(PMOD - 1)*(PMOD - 1 - X)/ 2
Quardrants
| IMOD = 2 - > PMOD - 1(水平) | NMOD = 1 - > PMOD - 1(垂直) |
| 1 ST左上= Q1 | 2 次右上= Q2 |
| 3 次左下= Q3 | 4 日右下方= Q4 |
| PMOD奇数IMOD边界(PMOD + 1)/ 2 | PMOD / 2之间PMOD甚至IMOD边界 |
| 之间NMOD边界(PMOD - 1)/ 2 | NMOD边境PMOD / 2 |
| IMOD边界从未ħ因为GCD(N,IMOD)!= 1 | IMOD即使再NMOD设置于H |
| Q1 [IMOD,NMOD] = - Q2 [N - IMOD,NMOD] | Q2 [IMOD,NMOD] = - Q1 [N - IMOD,NMOD] |
| Q1 [IMOD,NMOD] = Q3 [IMOD,PMOD - NMOD] | Q2 [IMOD,NMOD] = - Q3 [N - IMOD,PMOD - NMOD] |
| Q1 [IMOD,NMOD] = - Q4 [N - IMOD,PMOD - NMOD] | Q2 [IMOD,NMOD] = Q4 [IMOD,PMOD - NMOD] |
| Q3 [IMOD,NMOD] = Q1 [IMOD,PMOD - NMOD] | Q4 [IMOD,NMOD] = - Q1 [N - IMOD,PMOD - NMOD] |
| Q3 [IMOD,NMOD] = - Q2 [N - IMOD,PMOD - NMOD] | Q4 [IMOD,NMOD] = Q2 [IMOD,PMOD - NMOD] |
| Q3 [IMOD,NMOD] = - Q4 [N - IMOD,NMOD] | Q4 [IMOD,NMOD] = - Q3 [N - IMOD,NMOD] |
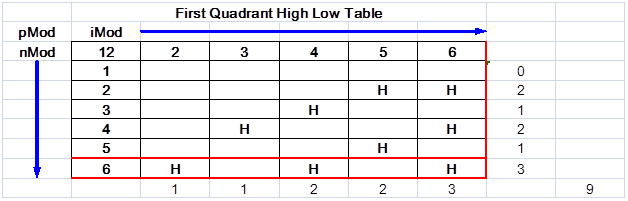
从图表4,“第一象限高低压表”和随后的表下面的关系可配制:
-
NMOD> 0,NMOD <PMOD哪里NMOD高= IMOD的数量 - 1
其中,IMOD> 1。
- 如果IMOD甚至&& NMOD = INT(PMOD / 2),那么NMOD =高
- 如果NMOD甚至&& IMOD = INT(PMOD / 2),那么NMOD =高
- 如果INT((1 * PMOD + 0)/ IMOD)= NMOD然后NMOD =高
- 如果INT((2 * PMOD + 1)/ IMOD)= NMOD然后NMOD =高
- 如果INT((3 * PMOD + 2)/ IMOD)= NMOD然后NMOD =高
- 诸如此类。
从“计算高低表”上述关系10可以被创建。见下面图表5。
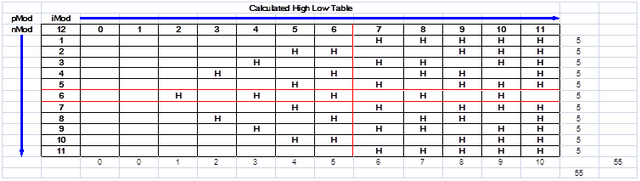
错误检测
在计算的高/低表检查错误,能够进行所计算出的与实际之间的序列检查。下面图表6检查是否存在错误的两个序列,并进行了人工修改,以反映错误作为一个例子。下面表7表示用于检测的误差相关联的PMOD。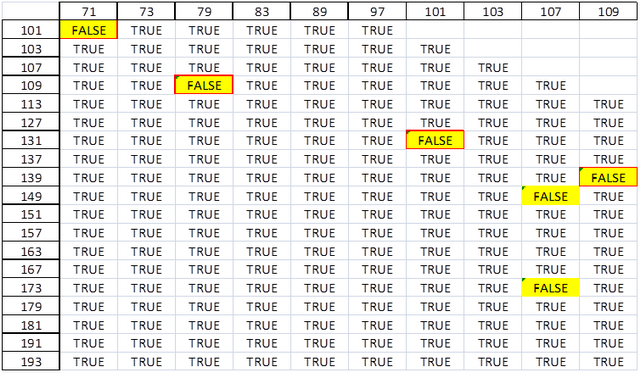
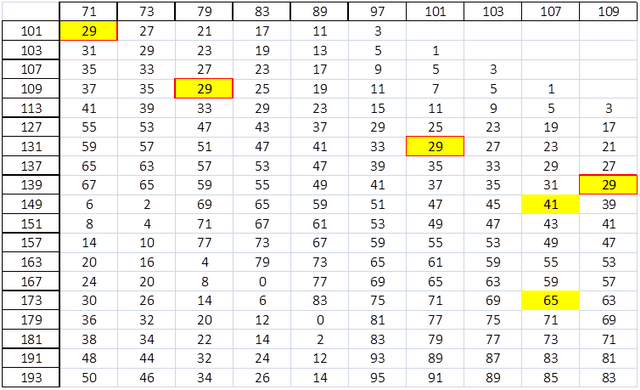
一旦其中已知发生错误的PMOD(图7),则参展8下面可以构造以指示序列中的误差的精确位置。
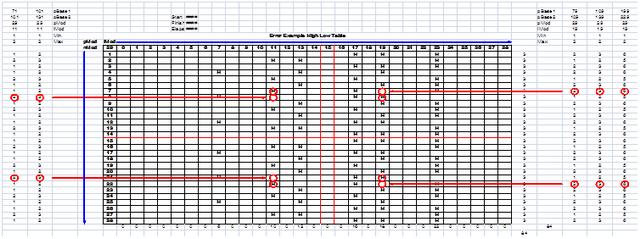
下面的图表9所示为PMOD删节算法扩张过程中= 29。
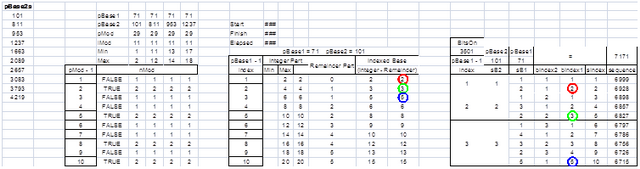
算法扩展过程
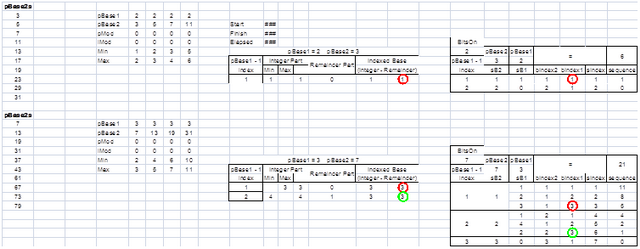
下面的图表10显示琐碎余算法的扩展过程,其中IMOD <2
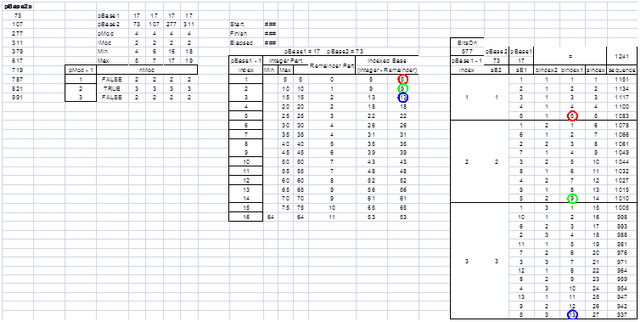
图表低于11显示了不平凡的地方余IMOD> 1删节算法扩展过程
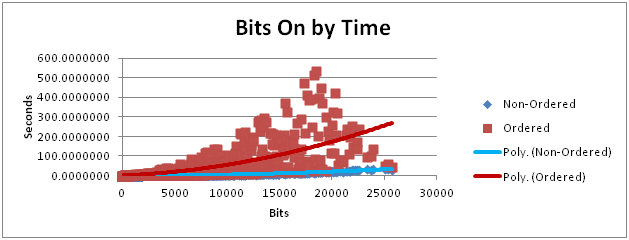
时间成本
下面的图表12表示订购的顺序同时产生它的时间成本。这个问题可能是:“为什么命令序列?” 一个答案是“它提供了一个工具来研究半贷二进制序列的解构。”
使用代码
该项目建成作为一个概念原型,并为更多的成品,例如不具有用户友好的错误检查。C#代码是专为64位系统。的Microsoft Office 2007是一个32位的环境下,需要的Excel-DNA被编译为32位。如果您希望这个项目在Microsoft Office版本是64位的运行,你会想重新编译的Excel-DNA为64位。该BigInterger库已被修改为任意大小的整数和例程从C#的BigInteger类已经被用于扩充到支持该项目所需的算法。我也修改了的BigInteger库有移位除法更高的准确性但计算速度的一些损失。目前已在图书馆BigInteger的其他几个支持例程,我已经修改,扩大其准确性或支持这个项目。该代码应该是准备去为C#项目时,Excel VBA和Excel电子表格进行试验。要在Excel中打开使用的BigInteger-packed.xll在电子表格中,并会有两个函数库的“BigInteger”和“数论”。要参考的BigInteger-packed.xll对于一些宏建在这个项目中使用的电子表格或其他VBA应用程序中使用的VBA环境是必需的。微软Access和Excel需要以下库的引用:
- Visual Basic应用程序
- 的Microsoft Access 12.0对象库
- OLE自动化
- 微软的Office 12.0 Access数据库引擎对象
- Microsoft ActiveX数据对象6.1库
- BigIntExcel
如果您使用的是.NET 4.0或更高版本可能要改变这个项目代码使用微软的数字图书馆。从我的研究中,除法算法的关键是精度和速度。
兴趣点
因为“这个代码是不是线程安全的RegisterSize ”功能,从而改变静态字段的值。通过消除该功能的过程应该是相当简单的在做这个项目线程安全的。目前我还没有探索在多CPU的环境中使用并行处理。一个BigInteger微软的Excel 2007中的最大尺寸为32,767十进制数字,如果超过此阈值将导致计算错误。